Due to the popularity of OneDrive, it has become an important source of evidence in forensics. Last week, Brian Maloney posted about his
research on reconstructing the folder tree from the usercid.dat files, and also
provided a script to do so. In this brief post, we explore the format of OneDrive Logs, and provide a tool to parse them. In subsequent posts, I will showcase use case scenarios.
Where to find them?
OneDrive logs have the extension .odl and are found in the user's profile folder at the following locations:
On Windows -
C:\Users\<USER>\AppData\Local\Microsoft\OneDrive\logs\
On macOS -
/Users/<USER>/Library/Logs/OneDrive/
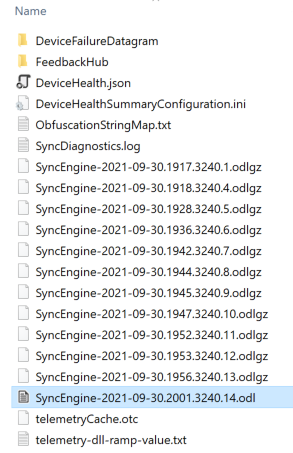
At these locations, there are usually 3 folders - Common, Business1 and Personal, each containing logs. As the name suggests Business1 is the OneDrive for Business version.
Figure 1 - Contents of Business1 folder
The .odl file is the currently active log, while the .odlgz files are older logs that have been compressed. Depending on which folder (and OS) you are in, you may also see .odlsent and .aodl files, which have a similar format.
What is in there?
These are binary files, and cannot be directly viewed in a text editor. Here is what a .odl file looks like in a hex editor.
Figure 2 - .odl file in a hex editor
It is a typical binary file format with a 256 byte header and data blocks that follow. Upon first inspection, it seems to be a log of all important function calls made by the program. Having this low level run log can be useful in certain scenarios where you don't have other logging and need to prove upload/download or synchronisation of files/folders or even a discovery of items which no longer exist on disk/cloud.
You do notice some funny looking strings (highlighted in red). More on that later..
The Format
With a bit of reverse engineering, the header format is worked out as follows:
struct {
char signature[8]; // EBFGONED
uint32 unk_version; // value seen = 2
uint32 unknown2;
uint64 unknown3; // value seen = 0
uint32 unknown4; // value seen = 1
char one_drive_version[0x40];
char os_version[0x40];
byte reserved[0x64];
} Odl_header;
The structures for the data blocks are as follows:
uint64 signature; // CCDDEEFF 0000000
uint64 timestamp; // Unix Millisecond time
uint32 code_file_name_len;
char code_file_name[code_file_name_len];
uint32 code_function_name_len;
char code_function_name[code_function_name_len];
In case of .odlgz files, the Odl_header is the same, followed by a single gzip compressed blob. The blob can be uncompressed to parse the Data_block structures.
Now, we can try to interpret the data. Leaving aside the few unknowns, the data block mainly consists of a timestamp (when event occurred), the function name that was called, the code file that function resides in and the parameters passed to the function. The parameters can be of various types like int, char, float, etc.. and that part hasn't been fully reverse engineered yet, but simply extracting the strings gives us a lot of good information. However the strings are obfuscated!
Un-obfuscating the strings
Since Microsoft uploads these logs to their servers for telemetry and debugging, they obfuscate anything that is part of a file/folder name or url string or username. However file extensions are not obfuscated. The ways this works is that the data identified to obfuscate is replaced by a word which is stored in a dictionary. The dictionary is available as the file ObfuscationStringMap.txt, usually in the same folder as the .odl files. To un-obfuscate, one simple needs to find and replace the strings with their original versions.
Figure 3 - Snipped of ObfuscationStringMap.txt
This is a tab separated file, stored as either UTF-8 or UTF-16LE depending on whether you are running macOS or Windows.
Now, referring back to the original funny looking string in Figure 2 -
/LeftZooWry/LogOneMug/HamUghVine/MuchDownRich/QuillRodEgg/KoiWolfTad/LawFlyOwl.txt
.. after un-obfuscating becomes ..
/Users/ykhatri/Library/Logs/OneDrive/Business1/telemetry-dll-ramp-value.txt
It is important to note that since extensions are not obfuscated, they can still provide valuable intel even if some or all of the parts in the path cannot be decoded.
Now this process seems easy, however not all obfuscated strings are file/folder names or parts of paths/urls. Some are multi line strings. Another problem is that the words (or keys to the dictionary) are reused! So you might see the same key several times in the ObfuscationStringMap. The thing to remember is that new entries get added at the top in this file, not at the bottom, so when reading a file, the first occurrence of a key should be the latest one. Also sometimes, the key is not found, as it's cleaned out after a period of time. Also there is no way to tell if an entry in the dictionary is stale or valid for a specific log file being parsed. All of this just means that the decoded strings need to be taken with a grain of salt.
Based on the above, a python script to parse the ODL logs is available
here. A snippet of the output produced by the script is shown below.
Figure 4 - output snippet
In a subsequent post, we'll go through the items of interest in these logs like Account linking/unlinking, uploads, downloads, file info, etc..